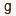|
|
Project 5: Evaluating Hypotheses
Exercise 5.4
You are about to test a hypothesis
h whose errorD(h)
is known to be in the range between 0.2 and 0.6.
-
What is the minimum number of examples ( n ) you must collect to
assure that the width of the two-sided 95% confidence interval
will be smaller that 0.1?
|
Let E ( error D ( h ) )
|
=
|
( 0.2 + 0.6 ) / 2
|
Note: I should have used 0.5
cause the function
f ( p ) = p ( 1 - p )
reaches max in the interval
[0, 1] ( and in [0.2, 0.6] )
when p = 0.5
|
=
|
0.4
|
|
95% interval width
|
=
|
2 * ( 1.96 * x )
|
|
x
|
=
|
square root [ 0.4 * ( 1 - 0.4 ) / n ]
|
|
for width
|
<
|
0.1
|
|
x
|
=
|
0.1 / ( 1.96 * 2 )
0.0255
|
|
|
=
|
0.0255
|
|
0.0255
|
=
|
square root [ 0.4 * ( 1 - 0.4 ) / n ]
|
|
0.00065025
|
=
|
( 0.4 * 0.6 ) / n
|
|
0.00065025
|
=
|
0.24 / n
|
|
n
|
=
|
0.24 / 0.00065025
|
|
n
|
=
|
370
|
(rounded from 369.088)
|

|