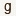|
|
Project 10.1: Reinforcement Learning
Exercise 13.2
Consider the deterministic grid world shown below with the
absorbing goal-state G.
Here the immediate rewards are 10 for the labeled transitions
and 0 for all unlabeled transitions.
_________________________________________________
| | | |
| | | |
| ---> ---> |
| <--- <--- |
| | | |
| ^ | | |10 | ^ | |
-------|-|--------------|--------------|-|-------
| | v | v | | v |
| | | |
| 10| G |10 |
| ---> <--- |
| | | |
|_______________|_______________|_______________|
|
-
-
*
Give the V* value for every state in this
grid world.
_________________________________________________
| | | |
| | | |
| 8 ---> 10 ---> 8 |
| <--- <--- |
| | | |
| ^ | | | | ^ | |
-------|-|--------------|--------------|-|-------
| | v | v | | v |
| | | |
| 10 | G | 10 |
| ---> <--- |
| | 0 | |
|_______________|_______________|_______________|
|
-
*
Give the Q ( s, a ) value for every
transition.
_________________________________________________
| | | |
| 8| 6.4| |
| ---> ---> |
| <--- <--- |
| |6.4 |8 |
| ^ |8 | |10 | ^ |8 |
-------|-|--------------|--------------|-|-------
| 6.4| v | v | 6.4| v |
| | | |
| | G | |
| ---> <--- |
| 10| 0 |10 |
|_______________|_______________|_______________|
|
-
Finally, show an optimal policy.
*
Use g = 0.8.
(Assume this is for all parts)
_________________________________________________
| | | |
| | | |
| | | |
| | | |
| | | |
| | | | | | |
--------|---------------|---------------|--------
| v | v | v |
| | | |
| | G | |
| ---> <--- |
| | | |
|_______________|_______________|_______________|
|
-
-
Suggest a change to the reward function
r ( s, a )
that alters the
Q ( s, a )
values, but does not alter the optimal policy.
Assuming that trivial things such as changing all the
reward values from 10 to some other constant or changing
g
or both are not what this is asking, so...
I suppose you could...
_________________________________________________
| | | |
| 1| 1| |
| ---> ---> |
| <--- <--- |
| |1 |1 |
| ^ |1 | |10 | ^ |1 |
-------|-|--------------|--------------|-|-------
| 1| v | v | 1| v |
| | | |
| 10| G |10 |
| ---> <--- |
| | | |
|_______________|_______________|_______________|
|
-
Suggest a change to
r ( s, a )
that alters
Q ( s, a )
but does not alter
V* ( s, a ).
_________________________________________________
| | | |
| | 1| |
| ---> ---> |
| <--- <--- |
| |1 | |
| ^ | | |10 | ^ | |
-------|-|--------------|--------------|-|-------
| 1| v | v | 1| v |
| | | |
| 10| G |10 |
| ---> <--- |
| | | |
|_______________|_______________|_______________|
|
-
Now consider applying the Q learning algorithm to this grid
world, assuming the table of Q_hat values is initialized to zero.
Assume the agent begins in the bottom left grid square and
then travels clockwise around the perimeter of the grid
until it reaches the absorbing goal state, completing
the first training episode.
-
Describe which Q_hat values are modified as a result of
this episode, and give their revised values.
Assume we start with the original grid world of this problem.
All Q_hats not specified are zero.
_________________________________________________
| | | |
| | | |
| ---> ---> |
| <--- <--- |
| | | |
| ^ | | | | ^ | |
-------|-|--------------|--------------|-|-------
| | v | v | | v |
| | | |
| | G |10 |
| ---> <--- |
| | | |
|_______________|_______________|_______________|
|
-
Answer the question again assuming the agent now performs
a second identical episode.
_________________________________________________
| | | |
| | | |
| ---> ---> |
| <--- <--- |
| | | |
| ^ | | | | ^ |8 |
-------|-|--------------|--------------|-|-------
| | v | v | | v |
| | | |
| | G |10 |
| ---> <--- |
| | | |
|_______________|_______________|_______________|
|
-
Answer it again for a third episode.
_________________________________________________
| | | |
| | 6.4| |
| ---> ---> |
| <--- <--- |
| | | |
| ^ | | | | ^ |8 |
-------|-|--------------|--------------|-|-------
| | v | v | | v |
| | | |
| | G |10 |
| ---> <--- |
| | | |
|_______________|_______________|_______________|
|
|

|